基于Matlab如何制作一个数独求解器
这篇“基于Matlab如何制作一个数独求解器”文章的知识点大部分人都不太理解,所以小编给大家总结了以下内容,内容详细,步骤清晰,具有一定的借鉴价值,希望大家阅读完这篇文章能有所收获,下面我们一起来看看这篇“基于Matlab如何制作一个数独求解器”文章吧。
1.完整效果


2.数独求解(错误示范)
首先我们先尝试如果只满足行、列、3x3块加和均为45的等式约束是否有效。即约束为:
每行和为45:

每列和为45:

每个3x3块和为45:

其中对此编写如下代码:
sudokuMat=[1 0 5 0 2 0 0 0 0 0 0 0 7 4 3 0 0 5 3 0 7 0 0 0 0 0 9 0 2 0 0 0 0 4 5 0 0 6 0 4 0 1 0 8 0 0 7 4 0 0 0 0 6 0 2 0 0 0 0 0 3 0 8 4 0 0 8 5 6 0 0 0 0 0 0 0 3 0 5 0 6]; % 记录原本各个数字所在位置,构造等式约束 n0Ind=find(sudokuMat~=0); Aeq1=zeros(length(n0Ind),81); for i=1:length(n0Ind) Aeq1(i,n0Ind(i))=1; end beq1=sudokuMat(sudokuMat~=0); % 行等式约束和列等式约束 Aeq2=zeros(9,81); Aeq3=zeros(9,81); for i=1:9 Aeq2(i,(i-1)*9+1:i*9)=1; Aeq3(i,i:9:81)=1; end beq2=ones(9,1).*45; beq3=ones(9,1).*45; % 3x3块等式约束 Aeq4=zeros(9,81); for i=1:3 for j=1:3 tmat=zeros(9,9); tmat((i-1)*3+1:i*3,(j-1)*3+1:j*3)=1; Aeq4((i-1)*3+j,:)=tmat(:)'; end end beq4=ones(9,1).*45; f=ones(1,81); % 不重要,随便设置 intcon=1:81; % 所有元素都要求为整数 lb=ones(81,1); % 下限为1 ub=ones(81,1).*9;% 上限为1 Aeq=[Aeq1;Aeq2;Aeq3;Aeq4]; beq=[beq1;beq2;beq3;beq4]; % 求解整数规划 X=intlinprog(f,intcon,[],[],Aeq,beq,lb,ub); % 重新 构造数独矩阵 X=reshape(X,[9,9])
那么,这么简单就能够解决数独了嘛???
当然不行。。。。
上述程序运行结果为:
1 8 5 6 2 9 9 1 4
2 9 9 7 4 3 5 1 5
3 1 7 1 4 9 8 3 9
7 2 1 8 9 4 4 5 5
9 6 1 4 1 1 9 8 6
8 7 4 1 8 9 1 6 1
2 1 9 1 9 3 3 9 8
4 9 8 8 5 6 1 3 1
9 2 1 9 3 1 5 9 6
可以发现我们的约束确实保证了三种加和都是45,但是不能保证同行、同列、同3x3块内不出现同样的数字,那咋办,总不能一个元素一个元素添加不相等信息吧、我们怎样能让矩阵包含更多的信息,更方便的阐述各个元素之间的联系呢?
3.数独求解(升维)
欸,我们原本是9x9大小的矩阵,要描述每个元素和同一行各个元素、和同一列各个元素之间的联系,一个很自然的想法就是升维!
将9×9的数独矩阵转化为9×9×9的三维矩阵(张量),此时X(i,j,k)=1意味原矩阵第i行,第j列的元素为k,整个整数规划从现在开始变成了0-1规划,要想同一行的数值都不一样,只需要所有的行纤维的和都是1,想要同一列的数值都不一样,只需要所有列纤维的和都是1,非常奇妙的,我们又把问题转换为了一个线性求和的问题,very amazing啊!
此时约束条件变为:
原矩阵每个小格子只能有一个数值:
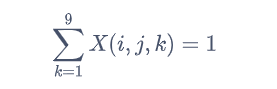
原矩阵每一行的各个数字均不同:
原矩阵每一列的各个数字均不同:
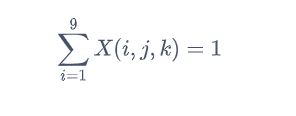
原矩阵每一个3x3块各个数字均不同:
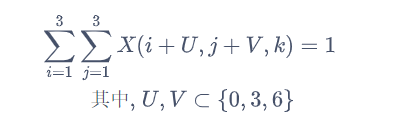
其中因此编写如下代码
sudokuMat=[1 0 5 0 2 0 0 0 0 0 0 0 7 4 3 0 0 5 3 0 7 0 0 0 0 0 9 0 2 0 0 0 0 4 5 0 0 6 0 4 0 1 0 8 0 0 7 4 0 0 0 0 6 0 2 0 0 0 0 0 3 0 8 4 0 0 8 5 6 0 0 0 0 0 0 0 3 0 5 0 6]; % 记录原本1所在位置,构造等式约束 n0Ind=find(sudokuMat~=0); Aeq0=zeros(length(n0Ind),9^3); for i=1:length(n0Ind) Aeq0(i,n0Ind(i)+(sudokuMat(n0Ind(i))-1)*81)=1; end % 每一行、列、管都只能有一个1 Aeq1=zeros(81,9^3); Aeq2=zeros(81,9^3); Aeq3=zeros(81,9^3); for i=1:9 for j=1:9 A1=zeros(9,9,9); A2=zeros(9,9,9); A3=zeros(9,9,9); A1(:,i,j)=1;Aeq1((i-1)*9+j,:)=A1(:)'; A2(i,:,j)=1;Aeq2((i-1)*9+j,:)=A2(:)'; A3(i,j,:)=1;Aeq3((i-1)*9+j,:)=A3(:)'; end end % 每个3x3的小矩阵都只能有一个1 Aeq4=zeros(81,9^3); for k=1:9 for i=1:3 for j=1:3 A4=zeros(9,9,9); A4((i-1)*3+1:i*3,(j-1)*3+1:j*3,k)=1; Aeq4((k-1)*9+(i-1)*3+j,:)=A4(:)'; end end end f=ones(1,9^3); % 不重要,随便设置 intcon=1:9^3; % 所有元素都要求为整数 lb=zeros(9^3,1);% 下限为0 ub=ones(9^3,1); % 上限为1 Aeq=[Aeq0;Aeq1;Aeq2;Aeq3;Aeq4]; beq=ones(size(Aeq,1),1); % 求解整数规划 X=intlinprog(f,intcon,[],[],Aeq,beq,lb,ub); % 重新 构造数独矩阵 X=reshape(X,[9,9,9]); resultMat=zeros(9,9); for i=1:9 resultMat=resultMat+X(:,:,i).*i; end resultMat
求解结果为:
LP:Optimal objective value is 81.000000.
Optimal solution found.
Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0
The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05
resultMat
1 8 5 6 2 9 7 3 4
6 9 2 7 4 3 8 1 5
3 4 7 1 8 5 6 2 9
9 2 1 3 6 8 4 5 7
5 6 3 4 7 1 9 8 2
8 7 4 5 9 2 1 6 3
2 5 6 9 1 7 3 4 8
4 3 9 8 5 6 2 7 1
7 1 8 2 3 4 5 9 6
历时 0.017170 秒,快到离谱。不得不说MATLAB规划算法还是niubility!
4.数字识别
想要做读取图片后识别数独矩阵的功能,但是本文做的只是一个基础款,没打算搞歪歪斜斜的数独题目图像,也没打算识别那些手写字体,于是既没有做角度矫正,也没搞CNN数字识别,大家学会基础款后可以自行添加相关功能,本文中的数字识别只是将图像切割后和数字库里几个图像进行对比:

只是做了简单的最小二乘法,求差值平方和,找到差异最小的图片,非常的简单,因此只能应对一些横平竖直的数独题目。
5.GUI / APP
反正都很简单,我就GUI版本和App designer版本都做了,以下仅展示 GUI 版本代码
function sudokuGui
% @author:slandarer
% GUI图窗创建
SDKFig=uifigure('units','pixels',...
'position',[300 100 450 500],...
'Numbertitle','off',...
'menubar','none',...
'resize','off',...
'name','数独求解器 1.0',...
'color',[1,1,1].*0.97);
SDKFig.AutoResizeChildren='off';
SDKAxes=uiaxes('Units','pixels',...
'parent',SDKFig,...
'PlotBoxAspectRatio',[1 1 1],...
'Position',[15 15 420 420],...
'Color',[0.99 0.99 0.99],...
'Box','on', ...
'XLim',[0 1],'YLim',[0 1],...
'XTick',[],'YTick',[]);
hold(SDKAxes,'on');
% SDKAxes.Toolbar.Visible='off';
% 按钮创建
uibutton(SDKFig,'Text','导 入 图 片','BackgroundColor',[0.31 0.58 0.80],'FontColor',[1 1 1],...
'FontWeight','bold','Position',[25,450,150,35],'FontSize',13,'ButtonPushedFcn',@loadPic);
uibutton(SDKFig,'Text','开 始 计 算','BackgroundColor',[0.31 0.58 0.80],'FontColor',[1 1 1],...
'FontWeight','bold','Position',[200,450,150,35],'FontSize',13,'ButtonPushedFcn',@solveSDK);
% =========================================================================
% 读取图像库内图像
path='数字图像库';
picInfor=dir(fullfile(path,'*.jpg'));
SDKPicSet{size(picInfor,1)}=[];
for n=1:size(picInfor,1)
tempPic=imread([path,'\',picInfor(n).name]);
SDKPicSet(n)={tempPic};
end
oriPic=[];
% 图像读取函数
function loadPic(~,~)
try
[filename, pathname] = uigetfile({'*.jpg;*.tif;*.png;*.gif','All Image Files';...
'*.*','All Files' });
oriPic=imread([pathname,filename]);
Lim=max(size(oriPic));
SDKAxes.XLim=[0 Lim];
SDKAxes.YLim=[0 Lim];
imshow(oriPic,'parent',SDKAxes)
catch
end
end
% 数独求解函数
function solveSDK(~,~)
% 提取数独矩阵及数独矩阵在图片中位置
[XLim,YLim,sudokuMat]=getMat(oriPic);
% 整数规划求解数独
resultMat=sudoku(sudokuMat);disp(resultMat)
% 补全数独图像
fillSDK(XLim,YLim,resultMat,sudokuMat)
end
% =========================================================================
% 提取数独矩阵
function [XLim,YLim,sudokuMat]=getMat(oriPic)
bw=~im2bw(oriPic);
deletedRange=round(((size(bw,1)+size(bw,2))/2)^2*0.00005);
bw=bwareaopen(bw,deletedRange);
% 定位数独表格
xDistrib=find(sum(bw,2)~=0);
yDistrib=find(sum(bw,1)~=0);
XLim=[xDistrib(1),xDistrib(end)];
YLim=[yDistrib(1),yDistrib(end)];
% 将图像进行切割并将数字填入矩阵
numPicSize=[round((XLim(2)-XLim(1)+1)/9),round((YLim(2)-YLim(1)+1)/9)];
selectedPic=imresize(bw(XLim(1):XLim(2),YLim(1):YLim(2)),9.*numPicSize);
sudokuMat=zeros(9,9);
for i=1:9
for j=1:9
% 切割出每个数字
numPic=selectedPic((i-1)*numPicSize(1)+1:i*numPicSize(1),(j-1)*numPicSize(2)+1:j*numPicSize(2));
numPic=imclearborder(numPic);
xDistrib=find(sum(numPic,2)~=0);
yDistrib=find(sum(numPic,1)~=0);
if ~any(xDistrib)||~any(yDistrib)% 若是方框是空的设置矩阵数值为0
sudokuMat(i,j)=0;
else
xLim=[xDistrib(1),xDistrib(end)];
yLim=[yDistrib(1),yDistrib(end)];
% 为了区分1和7,这里多删去一块
numPic=numPic(xLim(1):xLim(2)-round(0.1*(xLim(2)-xLim(1))),yLim(1):yLim(2));
xDistrib=find(sum(numPic,2)~=0);
yDistrib=find(sum(numPic,1)~=0);
xLim=[xDistrib(1),xDistrib(end)];
yLim=[yDistrib(1),yDistrib(end)];
numPic=numPic(xLim(1):xLim(2),yLim(1):yLim(2));
numPic=imresize(numPic,[70 40]);
% 最小二乘法选出最可能的数值
tempVarin=inf.*ones(1,size(picInfor,1));
% 循环和图像库中图像做差值并求平方和
for k=1:size(picInfor,1)
tempVarin(k)=sum((double(SDKPicSet{k})-numPic.*255).^2,[1,2]);
end
tempStr=picInfor(tempVarin==min(tempVarin)).name;
sudokuMat(i,j)=str2double(tempStr(1));
end
end
end
end
% -------------------------------------------------------------------------
% 整数规划求解数独
function resultMat=sudoku(sudokuMat)
% 记录原本1所在位置,构造等式约束
n0Ind=find(sudokuMat~=0);
Aeq0=zeros(length(n0Ind),9^3);
for i=1:length(n0Ind)
Aeq0(i,n0Ind(i)+(sudokuMat(n0Ind(i))-1)*81)=1;
end
% 每一行、列、管都只能有一个1
Aeq1=zeros(81,9^3);
Aeq2=zeros(81,9^3);
Aeq3=zeros(81,9^3);
for i=1:9
for j=1:9
A1=zeros(9,9,9);
A2=zeros(9,9,9);
A3=zeros(9,9,9);
A1(:,i,j)=1;Aeq1((i-1)*9+j,:)=A1(:)';
A2(i,:,j)=1;Aeq2((i-1)*9+j,:)=A2(:)';
A3(i,j,:)=1;Aeq3((i-1)*9+j,:)=A3(:)';
end
end
% 每个3x3的小矩阵都只能有一个1
Aeq4=zeros(81,9^3);
for k=1:9
for i=1:3
for j=1:3
A4=zeros(9,9,9);
A4((i-1)*3+1:i*3,(j-1)*3+1:j*3,k)=1;
Aeq4((k-1)*9+(i-1)*3+j,:)=A4(:)';
end
end
end
f=ones(1,9^3); % 不重要,随便设置
intcon=1:9^3; % 所有元素都要求为整数
lb=zeros(9^3,1);% 下限为0
ub=ones(9^3,1); % 上限为1
Aeq=[Aeq0;Aeq1;Aeq2;Aeq3;Aeq4];
beq=ones(size(Aeq,1),1);
% 求解整数规划
X=intlinprog(f,intcon,[],[],Aeq,beq,lb,ub);
% 重新 构造数独矩阵
X=reshape(X,[9,9,9]);
resultMat=zeros(9,9);
for i=1:9
resultMat=resultMat+X(:,:,i).*i;
end
end
% -------------------------------------------------------------------------
% 补全数独
function fillSDK(xLim,yLim,resultMat,sudokuMat)
for i=0:9
plot(SDKAxes,[yLim(1),yLim(1)]+i*(yLim(2)-yLim(1))/9,[xLim(1),xLim(2)],'Color',[0.29 0.65 0.85],'lineWidth',2)
plot(SDKAxes,[yLim(1),yLim(2)],[xLim(1),xLim(1)]+i*(xLim(2)-xLim(1))/9,'Color',[0.29 0.65 0.85],'lineWidth',2)
end
fontSize=18;
if (xLim(2)-xLim(1))>0.8*size(oriPic,1)
fontSize=36;
end
for i=1:9
for j=1:9
if (resultMat(j,i)~=0)&&(sudokuMat(j,i)==0)
text(SDKAxes,yLim(1)+(i-1)*(yLim(2)-yLim(1))/9+(yLim(2)-yLim(1))/9/2,...
xLim(1)+(j-1)*(xLim(2)-xLim(1))/9+(xLim(2)-xLim(1))/9/2,...
num2str(resultMat(j,i)),'HorizontalAlignment','center',...
'Color',[0.29 0.65 0.85],'fontWeight','bold','fontSize',fontSize)
end
end
end
end
end
以上就是关于“基于Matlab如何制作一个数独求解器”这篇文章的内容,相信大家都有了一定的了解,希望小编分享的内容对大家有帮助,若想了解更多相关的知识内容,请关注蜗牛博客行业资讯频道。
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:niceseo99@gmail.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。















评论