C语言中sizeof与整型数据存储及数据类型取值范围
这篇文章主要讲解了“C语言中sizeof与整型数据存储及数据类型取值范围”,文中的讲解内容简单清晰,易于学习与理解,下面请大家跟着小编的思路慢慢深入,一起来研究和学习“C语言中sizeof与整型数据存储及数据类型取值范围”吧!
1.关键字sizeof
sizeof 与 strlen 是我们日常打代码时经常使用到的两个“工具”。前者是求变量或者类型的大小(单位为字节),后者是求某一字符串的长度。我们很容易产生这样一个误解,即把 sizeof 和 strlen 归为函数一类。事实上 sizeof 并不是一个函数,它是一个操作符、关键字。我们通过一段代码证明它不是函数:
#include <stdio.h>
int main()
{
int n = 20;
printf("%d\n", sizeof(n));
printf("%d\n", sizeof(int));
printf("%d\n", sizeof n);
return 0;
}
我们注意到红线部分的 sizeof 后面的变量名没有加括号也能正常运行:

这就证明了 sizeof 它不是一个函数,而是一个操作符、关键字。
在这里顺便复习一下关于数组的知识,即数组名的两个特例(除了这两种情况其他任何时候数组名都表示数组首元素地址):
sizeof 内单独放数组名,其数组名表整个数组。
& 数组名,表取整个数组的地址。
由此也可以看出 sizeof 与函数的区别。
2.整型数据存储深入
变量的作用是在内存中开辟一块空间,而类型则决定了这块空间有多大。
我们可以与 sizeof 结合起来验证这个问题:
#include <stdio.h>
int main()
{
printf("%d\n", sizeof(char));
printf("%d\n", sizeof(short));
printf("%d\n", sizeof(int));
printf("%d\n", sizeof(long));
printf("%d\n", sizeof(long long));
return 0;
}
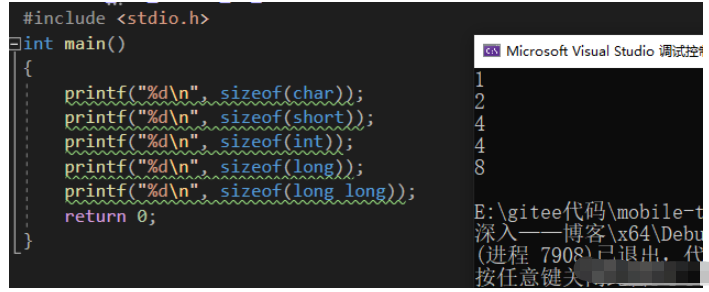
我们知道,计算机只能识别二进制,恰恰计算机系统又能把我们人类熟练使用的十进制转换成二进制,并且产生相应的原码、反码、补码。设计计算机的人设计出这样一套规则是非常巧妙的。
我们引出原码、反码、补码如何计算以及他们之间如何转换:
原码:将数字直接翻译成二进制得到的序列。
反码:在原码的基础上符号位(二进制序列的最高位,1表负数,0表负数)不变,替他位按位取反得到的序列。
补码:在反码的基础上加1。
补码计算回原码方法一:补码减1,然后符号位不变,其他位按位取反得到原码。
补码计算回原码方法二:补码符号位不变,其他位按位取反,然后加1。此方法与原码计算补码的方式是一样的,这样做的意义在于 CPU 进行数据处理时,只要设计一套计算方法就可以完成原码、反码、补码之间的相互转换。
那么具体的例子,在数据的存储——整形篇有讲到,这里就不赘述。
我们需要明白的是:数据存储到变量当中,不会受到类型的影响。什么意思呢?我们举个例子:
#include <stdio.h>
int main()
{
unsigned int p = -10;
return 0;
}
大家可以看到,我把一个负数存入到无符号的整型变量 p 中,这有些违反我们的直觉,无符号类型不是不存在负数的概念吗?事实上,不是程序出错,而是我们的直觉有问题。
我们在一开头便阐述了变量的作用在内存中开辟一块空间,而类型便是决定开辟多大的空间。就好比说,我们有 100 ,放在了我的荷包里,那我们能说我有 100 块吗?就算是钱,我们定义它是美元、港币、日元了吗?所以,我们可以把变量看成 100 ,类型看成是美元、港币、日元等等。
到这里,我们就可以清楚,数据的存储与变量的类型是没有关系的,变量的作用仅仅是开辟一块空间让我们的数据存储进去。聊到这里,不妨让我们再回顾一下,整型数据是如何存放在变量(内存)里面的。我们就以上面那段代码为例:

这里再提一嘴:虽然内存中存放的是二进制序列,但为了我们方便,内存还是会以十六进制的表现形式表现出来。
我们试探性往内存里面看 p 变量里面存的是什么东西:
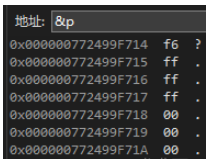
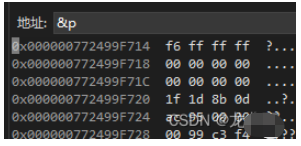
可以发现,内存里面的各种数据都对上了我们分析的结果,但是看起来有点“怪”。我们就来分析“怪”在哪里:
我们知道 int 类型是有 4 个字节的,那么数据占了 4 个字节没有问题。那么如果是以 1 列的形式查看地址,可以看到从上到下的地址是递增的。
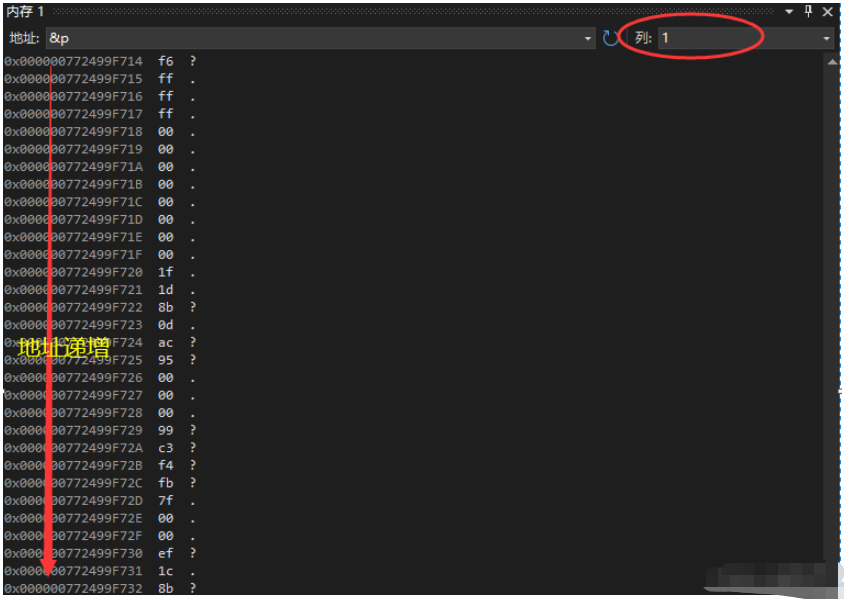
现在我们以 4 列的形式查看地址,可以看到从左往右地址递增,从上往下地址递增。
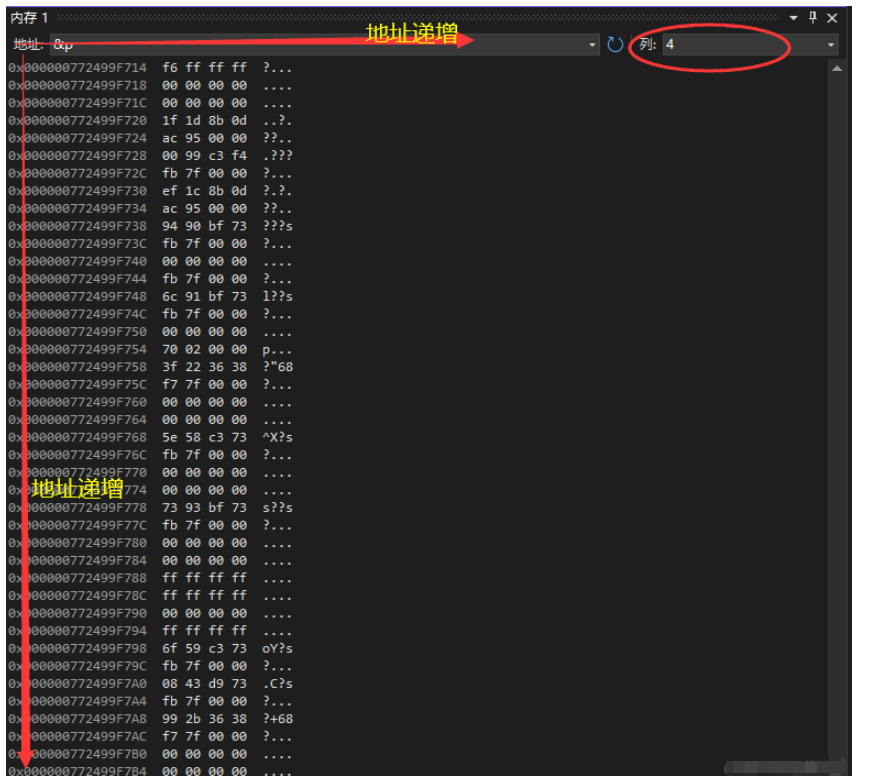
得出一个现象:f6 存在了我们的低地址处。
我们似乎可以这样做推导:

这样的存储模式我们叫做小端存储。为什么这样的模式叫做小端存储?我们使用这个案例来类比:
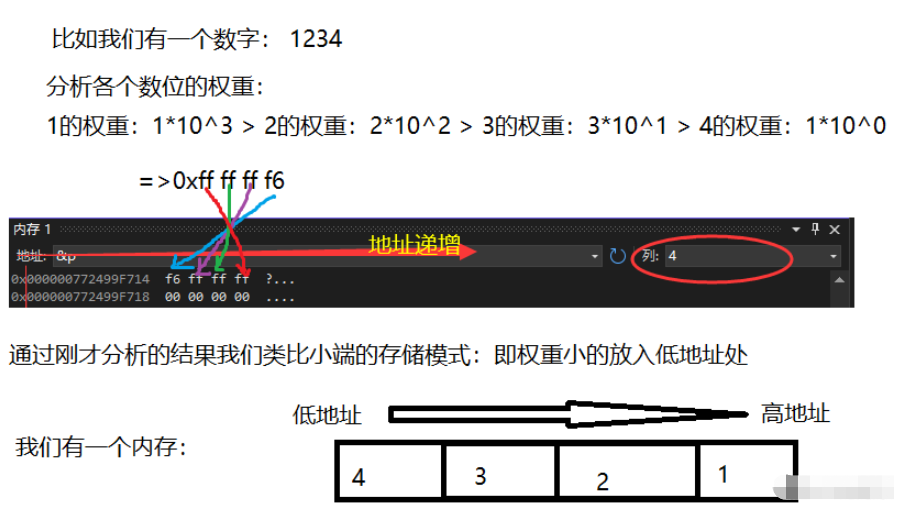
所以我们得出结论,小端与大端的存储模式可以定义为:
权重小的数位放入内存中的低地址处,权重大的放入内存中的高地址处,这样的存储模式叫小端存储。
权重小的数位放入内存中的高地址处,权重小的放入内存中的低地址处,这样的存储模式叫大端存储。
为什么会有这种看似复杂的存储模式?我们可以举一个例子:我们大家都吃过鸡蛋,有些人剥壳喜欢往小的那一头剥,有的人喜欢往大的那一头剥,也就是“剥鸡蛋”这个动作,没有统一的行为概念。硬件制作厂商也不例外,有的厂商想让数据的存储行为是小端,也有的厂商想让数据以大端的模式进行存储,只不过我们平时所接触的硬件,都是以小端模式存储字节序的。
我们讨论了数据的存储,现在我们来讨论一下数据的“取出”规则。
好比说我们举这个例子:
#include <stdio.h>
int main()
{
unsigned int p = -10;
printf("%u\n", p);
printf("%d\n", p);
return 0;
}
我们可以看到,对于 -10 存储在内存当中,我们第一次使用 %u 的形式将它从内存里拿出来,第二次使用 %d 的形式将它从内存中拿出来。
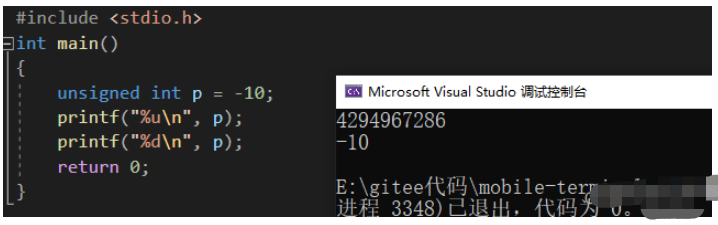
我们可以看到,对于不同类型的使用方式就会造成不同的结果。我们似乎可以这样断定:数据类型不会影响数据的存储,但一定会影响数据的取出(使用)。我们来分析一下为什么使用不同的类型打印能造成不同的结果:
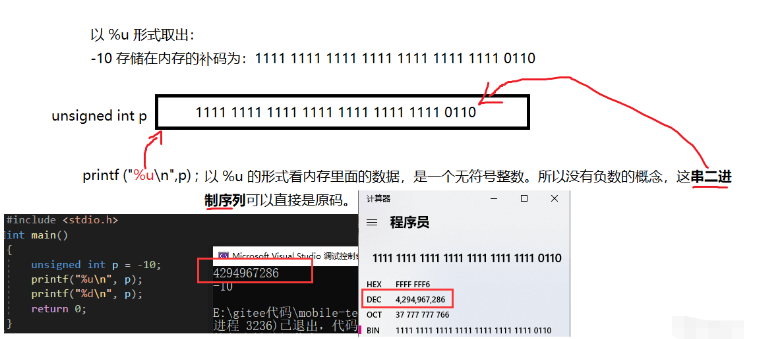

所以我们再总结一次:变量的数据类型不会对数据的存储产生影响(截断也不能算成是一种影响),但数据类型一定会影响数据的取出、使用。
3.数据类型取值范围深入
什么叫数据类型的取值范围?好比说我们有这样一个例子:

那么我们取 C 语言中大小最小的数据类型 char 来讨论数据类型的取值范围。
我们知道,char 类型只有 1 个字节,它有 8 个比特位。无符号类型的 char 我们就不做讨论,我们重点讨论无符号类型的 char 。那么 8 个比特位,能有多少种排列组合?能从什么值取到什么值?

那么通过演绎推理,得出来排列组合得个数,有什么意义呢?可以确定八个比特位能存放多少个数字。例如两个比特位能存放 4 个数字,三个比特位能存放 8 个数字,八个比特位能存放 256 个数字。
现在我们的重点在于:char 类型的八个比特位,能存哪 256 个数字?

可以看到这个结果,取值范围似乎是 [-127,127] ,但是这个区间里面只有 255 个数,那我们理论推导出来的结果是 256 个数,是我们推导错了吗?其实不然,我们应该注意 1000 0000 后面的那个问号:如果这串二进制序列真表示 0 了,那么就有两个 0 了,但是在计算机在考虑取值范围的时候,是不会浪费任何一个比特位来存放相同的数字的。
那么既然冲突了,就要在两个边界任意一端扩充。那么是 128 还是 -128 呢?只能是 -128 。在这里,我们就已经踏入计算机的知识边界了,为什么只能是 -128 它是个数学问题,就好比为什么会设计出原码、反码、补码一样,我们是无法理解设计计算机的人为什么会这样设计的。所以在这里只需记住,char 类型的取值范围是 [-2^7,2^7-1] 。那么我们类比出来 short 类型的取值范围是 [-2^15,2^15-1] , int 类型的取值范围是 [-2^31,2^31-1] ……
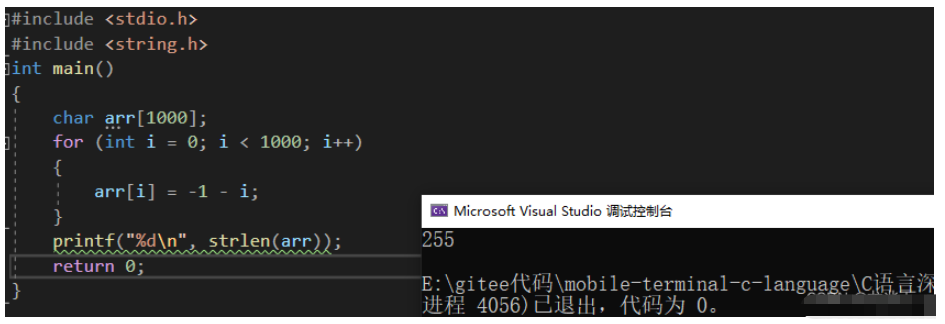
我们来看一个非常经典的例题:
#include <stdio.h>
#include <string.h>
int main()
{
char arr[1000];
for (int i = 0; i < 1000; i++)
{
arr[i] = -1 - i;
}
printf("%d\n", strlen(arr));
return 0;
}
那么这道题要我们输出 arr 数组的长度是什么意思呢?我们再好好想想 strlen 。strlen 是求字符串长度,我们模拟实现过 strlen 的工作机制,知道遇到 '\0' 时就停止,返回 '\0' 之前的字符长度。那么 '\0' 就是数学意义上的 0 。其 '\' 是转义字符,如果仅仅写 '0' 的话,那么这个 '0' 并非数学意义上的 0 ,而是一个字符 0 。
好的,那我们知道这段代码会循环 1000 次对数组赋值。实际上我们的输出的要求是:输出 '\0' 出现之前的字符长度。我们可以这么运算:

我们通过计算,可以计算出当数组下标为 255 时,元素存储的是 0 ,即代表存储的是 '\0' ,那么 strlen 碰到 '\0' 时就会停止。那么数组下标为 255 ,那数组下标 0~255 有 256 个元素,舍弃一个 '\0' ,即剩下 255 个有效字符。所以最后输出 255 。
感谢各位的阅读,以上就是“C语言中sizeof与整型数据存储及数据类型取值范围”的内容了,经过本文的学习后,相信大家对C语言中sizeof与整型数据存储及数据类型取值范围这一问题有了更深刻的体会,具体使用情况还需要大家实践验证。这里是蜗牛博客,小编将为大家推送更多相关知识点的文章,欢迎关注!
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:niceseo99@gmail.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。















评论