C++中怎么正确使用hashmap
这篇“C++中怎么正确使用hashmap”文章的知识点大部分人都不太理解,所以小编给大家总结了以下内容,内容详细,步骤清晰,具有一定的借鉴价值,希望大家阅读完这篇文章能有所收获,下面我们一起来看看这篇“C++中怎么正确使用hashmap”文章吧。
hash冲突的解决方案
首先回顾一下hash冲突的解决方案有哪些。
Open addressing
open addressing是通过探测或者搜索数组的方法找到未使用的bucket来解决hash冲突的。
优点:
* 当hash冲突很小的时候,只需要访问对应的bucket就能获得对应的pair<key, value>,不需要再查找额外的数据结构,性能较好。
缺点:
* 对hash函数的要求比较高,否则当hash冲突很大的时,查找速度会很慢。
Separate chaining
或者叫closed addressing,当发生hash冲突时需要通过额外的数据结构来处理,比如链表或者红黑树。
优点:
* hash冲突处理简单,比如采用链表来解决hash冲突的话,添加节点的时候直接在链表后面添加即可。
* 对hash函数要求会低一点,即便冲突稍微大一点,也能把查找速度控制得比较好。
缺点:
* 由于需要额外的数据结构处理,性能在一般情况下不如Open addressing。
STL采用的是Separate chaining的方案。使用链表挂在bucket上解决冲突,当链表超过一定长度时转换为红黑树。
Flat Or Node
一般的开源库都会提供两种memory layout,一种叫flat,另一种叫node。
Flat
flat实现是指存储pair<key, value>的时候是直接存到对应的节点上。
优点:
* 对比node少一次寻址,对cache更加友好,查找速度会更高。
缺点:
* 对象不稳定,rehash的时候对象地址会修改,如果对象是个大结构的话rehash时的开销会比node要大。
Node
node实现是指在节点上只存储pair<key, value>的地址。而pair<key, value>则存储在另一块内存上。
优点:
* 对象稳定,rehash的时候对象地址不修改,且rehash的效率不会被结构体影响。
缺点:
* 查找多一次寻址,对cache不友好,查找速度会比flat要慢。
STL用的是Node的实现。每个pair<key, value>都是stable的。
使用建议
在hash冲突上,大部分的开源实现都选择了Open addressing这种方式,毕竟理论性能会更好,而flat和node则是两种实现都会提供。结合上面说的各种优缺点,我们可以简单得出一套通用的方案。
首先考虑下面几个点:
1. 是否可以一开始就可以确定好容量。
2. key的copy开销是否很大。
3. value的copy开销是否很大。
4. value的地址不稳定是否会影响代码逻辑。
可以简单归纳为以下四种情况:
情况1:value可以是不稳定的,而且容量是已知的,可以一开始确定。
推荐:使用flat实现,通过一开始reserve两倍的size来减少rehash带来的开销。
情况2:value可以是不稳定的,容量未知,key和value的copy开销很小。
推荐:使用flat实现。
情况3:value可以是不稳定的,容量未知,key的copy开销很小但value的copy开销很大。
推荐:使用flat实现,value使用unique_ptr包裹起来。
其他情况均使用node结构。
RobinHood
上面提到的规则基本可以适用大部分情况,但也不是没有例外,比如笔者在用这套规则去测试robinhood的性能的时候发现行不通,robinhood在绝大部分情况下都是node的实现性能会更高,除非value是个十分简单的结构。通过分析发现,这主要是因为以下两个原因:
1.robinhood在emplace的时候会有移动pair<key, value>的操作,这使得如果pair<key, value>的copy代价很高,性能会大打折扣。
2.robinhood实现了自己的allocator来分配node的内存,使得调用malloc的次数大约为log(n)次,并且内存连续的情况会变多,对CPU Cache比一般的node实现要友好。
具体我们可以看看源代码,首先是emplace的实现。
void nextWhileLess(InfoType* info, size_t* idx) const noexcept {
// unrolling this by hand did not bring any speedups.
while (*info < mInfo[*idx]) {
next(info, idx);
}
}
// Finds key, and if not already present prepares a spot where to pot the key & value.
// This potentially shifts nodes out of the way, updates mInfo and number of inserted
// elements, so the only operation left to do is create/assign a new node at that spot.
template <typename OtherKey>
std::pair<size_t, InsertionState> insertKeyPrepareEmptySpot(OtherKey&& key) {
for (int i = 0; i < 256; ++i) {
size_t idx{};
InfoType info{};
// 找到对应key的info
keyToIdx(key, &idx, &info);
// 跳过distance大于自己的
nextWhileLess(&info, &idx);
// while we potentially have a match
while (info == mInfo[idx]) {
// distance相等的情况需要判key是不是已经存在了
if (WKeyEqual::operator()(key, mKeyVals[idx].getFirst())) {
// key already exists, do NOT insert.
// see http://en.cppreference.com/w/cpp/container/unordered_map/insert
return std::make_pair(idx, InsertionState::key_found);
}
next(&info, &idx);
}
// unlikely that this evaluates to true
if (ROBIN_HOOD_UNLIKELY(mNumElements >= mMaxNumElementsAllowed)) {
if (!increase_size()) {
return std::make_pair(size_t(0), InsertionState::overflow_error);
}
continue;
}
// key not found, so we are now exactly where we want to insert it.
// 此时的位置原来的distance一定是小于当前的distance
auto const insertion_idx = idx;
auto const insertion_info = info;
if (ROBIN_HOOD_UNLIKELY(insertion_info + mInfoInc > 0xFF)) {
mMaxNumElementsAllowed = 0;
}
// find an empty spot
// 找到下一个空白的位置
while (0 != mInfo[idx]) {
next(&info, &idx);
}
// 如果当前的位置不是空白的,则把当前位置->下一个空白位置的所有元素往后移
if (idx != insertion_idx) {
shiftUp(idx, insertion_idx);
}
// put at empty spot
mInfo[insertion_idx] = static_cast<uint8_t>(insertion_info);
++mNumElements;
return std::make_pair(insertion_idx, idx == insertion_idx
? InsertionState::new_node
: InsertionState::overwrite_node);
}
// enough attempts failed, so finally give up.
return std::make_pair(size_t(0), InsertionState::overflow_error);
}
template <typename OtherKey, typename... Args>
std::pair<iterator, bool> try_emplace_impl(OtherKey&& key, Args&&... args) {
ROBIN_HOOD_TRACE(this)
auto idxAndState = insertKeyPrepareEmptySpot(key);
switch (idxAndState.second) {
case InsertionState::key_found:
break;
case InsertionState::new_node:
::new (static_cast<void*>(&mKeyVals[idxAndState.first])) Node(
*this, std::piecewise_construct, std::forward_as_tuple(std::forward<OtherKey>(key)),
std::forward_as_tuple(std::forward<Args>(args)...));
break;
case InsertionState::overwrite_node:
mKeyVals[idxAndState.first] = Node(*this, std::piecewise_construct,
std::forward_as_tuple(std::forward<OtherKey>(key)),
std::forward_as_tuple(std::forward<Args>(args)...));
break;
case InsertionState::overflow_error:
throwOverflowError();
break;
}
return std::make_pair(iterator(mKeyVals + idxAndState.first, mInfo + idxAndState.first),
InsertionState::key_found != idxAndState.second);
}
这里robinhood有一个很神奇的操作,它在info里面存了一个distance,这个distance表示当前元素所在位置与初始位置的距离,简单举例,假设我插入了4个key,分别为a,b,c,d。
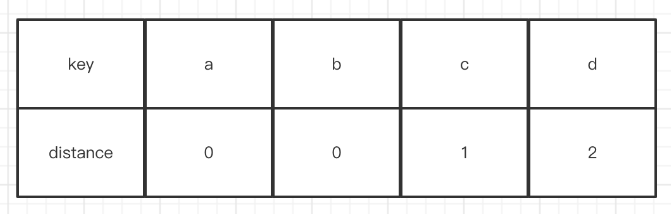
sequence1:插入a,hash(a) == 0,此时index0是空的,直接插入。它的distance(0, 0) == 0。
sequence2:插入b,hash(b) == 1,此时index1是空的,直接插入。它的distance(1, 1) == 0。
sequence3:插入c,hash(c) == 1,此时index1存在,那么找到下一个位置2插入,它的distance(1, 2) == 1。
sequence4:插入d,hash(d) == 1,此时index1和2都存在,找到位置3插入,它的distance(1, 3) == 2。
至于它的移动操作是怎么来的呢,假设基于上面的流程此时再加一个插入元素e的操作,并且这时候hash(e) == 0,首先是index0,发现这个位置两者的distance是相同,所以跳过看下一个。而index1则满足条件(新的距离>当前b这个key的距离),所以会把e放到index1这个位置,并且找到下一个空白的位置index4,然后把c, d这两个元素后移,最终会变成下面这个图。
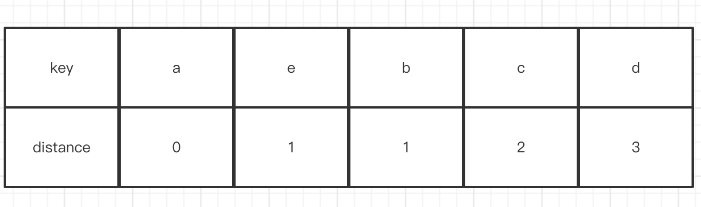
分配内存这块就比较简单了。
T* allocate() {
T* tmp = mHead;
if (!tmp) {
tmp = performAllocation();
}
mHead = *reinterpret_cast_no_cast_align_warning<T**>(tmp);
return tmp; }
ROBIN_HOOD(NOINLINE) T* performAllocation() {
size_t const numElementsToAlloc = calcNumElementsToAlloc();
// alloc new memory: [prev |T, T, ... T]
size_t const bytes = ALIGNMENT + ALIGNED_SIZE * numElementsToAlloc;
ROBIN_HOOD_LOG("std::malloc " << bytes << " = " << ALIGNMENT << " + " << ALIGNED_SIZE
<< " * " << numElementsToAlloc)
add(assertNotNull<std::bad_alloc>(std::malloc(bytes)), bytes);
return mHead;
}
ROBIN_HOOD(NODISCARD) size_t calcNumElementsToAlloc() const noexcept {
auto tmp = mListForFree;
size_t numAllocs = MinNumAllocs;
while (numAllocs * 2 <= MaxNumAllocs && tmp) {
auto x = reinterpret_cast<T***>(tmp);
tmp = *x;
numAllocs *= 2;
}
return numAllocs;
}
每次都分配比原来更多的内存,所以大概是分配log(n)次。
所以如果是用的robinhood,笔者建议除非你的pair<key, value>真的是非常简单的结构,否则都是用node实现会好一点。或者你可以交给robinhood自己判断,不显示指定使用flat还是node,robinhood的模板会自动根据你的size去判断去使用哪个实现。
using unordered_map =
detail::Table<sizeof(robin_hood::pair<Key, T>) <= sizeof(size_t) * 6 &&
std::is_nothrow_move_constructible<robin_hood::pair<Key, T>>::value &&
std::is_nothrow_move_assignable<robin_hood::pair<Key, T>>::value,
MaxLoadFactor100, Key, T, Hash, KeyEqual>;
template <bool IsFlat, size_t MaxLoadFactor100, typename Key, typename T, typename Hash,
typename KeyEqual>
class Table
: public WrapHash<Hash>,
public WrapKeyEqual<KeyEqual>,
detail::NodeAllocator<
typename std::conditional<
std::is_void<T>::value, Key,
robin_hood::pair<typename std::conditional<IsFlat, Key, Key const>::type, T>>::type,
4, 16384, IsFlat> {}
RobinHood VS Absl
这里附带上一个简单的benchmark测试robinhood和absl的性能,测试的key是uint32_t类型,value是个120size的结构。测试代码如下
//
// Created by victorika on 2022/10/14.
//
#include "absl/container/flat_hash_map.h"
#include "absl/container/node_hash_map.h"
#include <vector>
#include <cstdio>
#include <iostream>
#define ANKERL_NANOBENCH_IMPLEMENT
#include "riemann/3rd/nanobench/nanobench.h"
#include "robin_hood.h"
/**
* 测试结构
*/
struct TestStruct {
uint32_t* a;
std::vector<uint32_t> b, c, d;
std::string e, f, g;
uint32_t h, i, j;
};
void TestEmplace() {
ankerl::nanobench::Bench bench;
bench.minEpochIterations(50);
bench.title("Benchmarking rare value emplace");
bench.run("absl_flat", [&] {
absl::flat_hash_map<uint32_t, TestStruct> m;
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, TestStruct());
}
});
bench.run("absl_flat_and_set_value_pointer", [&] {
absl::flat_hash_map<uint32_t, std::unique_ptr<TestStruct>> m;
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, std::make_unique<TestStruct>());
}
});
bench.run("absl_node", [&] {
absl::node_hash_map<uint32_t, TestStruct> m;
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, TestStruct());
}
});
bench.run("absl_flat_reserve", [&] {
absl::flat_hash_map<uint32_t, TestStruct> m;
m.reserve(20000);
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, TestStruct());
}
});
bench.run("absl_flat_and_set_value_pointer_reserve", [&] {
absl::flat_hash_map<uint32_t, std::unique_ptr<TestStruct>> m;
m.reserve(20000);
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, std::make_unique<TestStruct>());
}
});
bench.run("absl_node_reserve", [&] {
absl::node_hash_map<uint32_t, TestStruct> m;
m.reserve(20000);
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, TestStruct());
}
});
bench.run("robinhood_flat", [&] {
robin_hood::unordered_flat_map<uint32_t, TestStruct> m;
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, TestStruct());
}
});
bench.run("robinhood_flat_and_set_value_pointer", [&] {
robin_hood::unordered_flat_map<uint32_t, std::unique_ptr<TestStruct>> m;
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, std::make_unique<TestStruct>());
}
});
bench.run("robinhood_node", [&] {
robin_hood::unordered_node_map<uint32_t, TestStruct> m;
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, TestStruct());
}
});
bench.run("robinhood_flat_reserve", [&] {
robin_hood::unordered_flat_map<uint32_t, TestStruct> m;
m.reserve(20000);
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, TestStruct());
}
});
bench.run("robinhood_flat_and_set_value_pointer_reserve", [&] {
robin_hood::unordered_flat_map<uint32_t, std::unique_ptr<TestStruct>> m;
m.reserve(20000);
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, std::make_unique<TestStruct>());
}
});
bench.run("robinhood_node_reserve", [&] {
robin_hood::unordered_node_map<uint32_t, TestStruct> m;
m.reserve(20000);
for (int i = 0; i < 10000; i++) {
m.try_emplace(i, TestStruct());
}
});
}
void TestSearch() {
absl::flat_hash_map<uint32_t, TestStruct> m1;
absl::flat_hash_map<uint32_t, std::unique_ptr<TestStruct>> m2;
absl::node_hash_map<uint32_t, TestStruct> m3;
robin_hood::unordered_flat_map<uint32_t, TestStruct> m4;
robin_hood::unordered_flat_map<uint32_t, std::unique_ptr<TestStruct>> m5;
robin_hood::unordered_node_map<uint32_t, TestStruct> m6;
for (int i = 0; i < 10000; i++) {
m1.try_emplace(i, TestStruct());
m2.try_emplace(i, std::make_unique<TestStruct>());
m3.try_emplace(i, TestStruct());
m4.try_emplace(i, TestStruct());
m5.try_emplace(i, std::make_unique<TestStruct>());
m6.try_emplace(i, TestStruct());
}
ankerl::nanobench::Bench bench;
bench.minEpochIterations(50);
std::vector<uint32_t> key_v;
key_v.resize(10000);
bench.title("Benchmarking rare value search");
bench.run("absl_flat_normal", [&] {
for (int i = 0; i < 10000; i++) {
auto it = m1.find(i);
key_v[i] = it->first;
}
});
bench.run("absl_flat_unique_ptr", [&] {
for (int i = 0; i < 10000; i++) {
auto it = m2.find(i);
key_v[i] = it->first;
}
});
bench.run("absl_node", [&] {
for (int i = 0; i < 10000; i++) {
auto it = m3.find(i);
key_v[i] = it->first;
}
});
bench.run("robinhood_flat_normal", [&] {
for (int i = 0; i < 10000; i++) {
auto it = m4.find(i);
key_v[i] = it->first;
}
});
bench.run("robinhood_unique_ptr", [&] {
for (int i = 0; i < 10000; i++) {
auto it = m5.find(i);
key_v[i] = it->first;
}
});
bench.run("robinhood_node", [&] {
for (int i = 0; i < 10000; i++) {
auto it = m6.find(i);
key_v[i] = it->first;
}
});
}
void TestIterator() {
absl::flat_hash_map<uint32_t, TestStruct> m1;
absl::flat_hash_map<uint32_t, std::unique_ptr<TestStruct>> m2;
absl::node_hash_map<uint32_t, TestStruct> m3;
robin_hood::unordered_flat_map<uint32_t, TestStruct> m4;
robin_hood::unordered_flat_map<uint32_t, std::unique_ptr<TestStruct>> m5;
robin_hood::unordered_node_map<uint32_t, TestStruct> m6;
for (int i = 0; i < 10000; i++) {
m1.try_emplace(i, TestStruct());
m2.try_emplace(i, std::make_unique<TestStruct>());
m3.try_emplace(i, TestStruct());
m4.try_emplace(i, TestStruct());
m5.try_emplace(i, std::make_unique<TestStruct>());
m6.try_emplace(i, TestStruct());
}
ankerl::nanobench::Bench bench;
bench.minEpochIterations(50);
std::vector<uint32_t> key_v;
key_v.resize(10000);
bench.title("Benchmarking rare value iterator");
bench.run("absl_flat_normal", [&] {
int i = 0;
for (auto &[key, value] : m1) {
key_v[i] = key;
}
});
bench.run("absl_flat_unique_ptr", [&] {
int i = 0;
for (auto &[key, value] : m2) {
key_v[i] = key;
}
});
bench.run("absl_node", [&]() {
int i = 0;
for (auto &[key, value] : m3) {
key_v[i] = key;
}
});
bench.run("robinhood_flat_normal", [&] {
for (int i = 0; i < 10000; i++) {
auto it = m4.find(i);
key_v[i] = it->first;
}
});
bench.run("robinhood_flat_unique_ptr", [&] {
for (int i = 0; i < 10000; i++) {
auto it = m5.find(i);
key_v[i] = it->first;
}
});
bench.run("robinhood_node", [&] {
for (int i = 0; i < 10000; i++) {
auto it = m6.find(i);
key_v[i] = it->first;
}
});
}
int main() {
std::cout << "size=" << sizeof(TestStruct) << std::endl;
TestEmplace();
TestSearch();
TestIterator();
}
测试结果
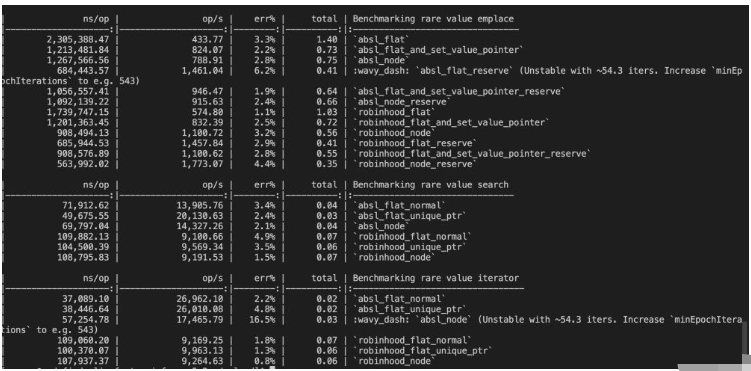
可以看到,在value copy rare的场景,absl的性能完全遵循上面提到的规则,而robinhood在这种情况下,emplace+construct+deconstruct是node更快,查找和遍历几乎和flat没区别。横向对比absl和robinhood两者的话,在查找和遍历上都是absl更快,emplace+construct+deconstruct在优化到极致的情况下两者差不多,robinhood并没有比absl快多少。当然,这只是简单测试,针对key类型不同的场景可能两者速度不太一样,具体就需要更加详细的benchmark了。
笔者也尝试过极简类型的场景,结论也没有违背上面的规则,都是flat速度远大于node。
建议:从两者里面选择的话,如果选型是用flat的话建议用absl,是node的话建议用robinhood。
以上就是关于“C++中怎么正确使用hashmap”这篇文章的内容,相信大家都有了一定的了解,希望小编分享的内容对大家有帮助,若想了解更多相关的知识内容,请关注蜗牛博客行业资讯频道。
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:niceseo99@gmail.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。














评论